我自己目前做的记忆研究,也才做了 5 年左右,谈不上付出一生。前排的几位老师,是真的数十年如一日地将自己奉献给他们所热爱的科研事业。从我自己的经历来看他们的回答,感觉已经很充分了。我也写不出什么更有新意的回答,就分享分享我自己的科研故事吧。
我是如何在本科期间发表顶会论文的?
泻药,人在清远,刚开电脑,大四期间发表一篇 ACM KDD 顶会论文[1],一篇 CCF T1 中文期刊论文[2],一篇 IEEE TKDE 顶刊论文[3],目前维护的开源项目已经达到 2.6k stars[4]。
KDD 论文中文版:KDD’22 | 墨墨背单词:基于时序模型与最优控制的记忆算法 [AI+教育]
TKDE 论文中文版:IEEE TKDE 2023 | 墨墨背单词:通过捕捉记忆动态,优化间隔重复调度
开源项目:GitHub – open-spaced-repetition/fsrs4anki: A modern Anki custom scheduling based on Free Spaced Repetition Scheduler algorithm
由于我的科研经历实在过于诡异(歪门邪道),所以我也不懂大多数人做科研到底是怎么样的,更不用说他们是怎么发论文的了。
我也不像那些本科大佬,既没有竞赛经历,也不是什么牛导的弟子,更没有牛逼的师兄。我沉溺于自己的研究世界里,要是没发论文的话,或许被大家当作民科也没什么毛病。
我的研究方向是间隔重复[5]调度优化(说人话,就是通过调整复习安排,提高学生的记忆效率),细分下来就是对学生的记忆进行建模,然后根据记忆模型和优化目标设计算法,寻找最优记忆策略。这两篇论文写作都只花了不到 1 个月,但背后是我长达 4 年的探索与思考。和别的科研工作者相比,说我是个「异端」也不为过,毕竟在同行评议和非升即走盛行的当下,谁会冒着大概率发表不出论文的压力和风险,先从非学术内容开始寻找自己的研究方向呢?所以我的经历可能没有什么参考价值,但我也相信世界上存在与曾经的我处境类似的人,希望我的这篇回忆能够帮助到你。
引发兴趣
若要溯源这两篇论文的起源,我想从我对间隔重复这一领域产生兴趣说起。虽然在绝大多数人看来,科研是非常抽象且神秘的。但科研作为一项人类活动,它一定是跟具体的人、具体的生活、具体的兴趣连在一起。
我第一次接触间隔重复大约在 2017 年,那时我从一个非常讨厌复习的高中生,逐步转变成一个想要提高复习效率的高中生。2017 年 4 月,我在知乎上搜索复习安排软件,鬼使神差地通过 @余时行 的回答找到了 Anki,一款开源的间隔重复软件。一年多的 Anki 使用,辅助我提高了一百多分[6],最终考进哈工深的计算机系,这让我对这一小众软件提高复习效率的原理产生了兴趣。
然后,我就通过 Anki 了解到了间隔重复、间隔效应、测试效应等一系列认知心理学相关的知识。正好 Anki 是开源软件,我又正好刷到知乎上 Anki 算法相关的问题,于是就去阅读了 Anki 的源码,写了相关文章[7]。那个时候差不多是 2018 年 8 月。
了解传统
阅读源码,查阅手册,我才了解到 Anki 的复习算法是 SuperMemo 2 算法的变体,这不经让我对 SuperMemo 也好奇起来。不过那个时候的我还在忙于推广 Anki,卖着 Anki 笔记挣钱,以及做模仿 Anki 的产品设计,这些探索暂时搁置了下来。直到 2019 年年底,我在创业失败中深感自己的能力不足,想要静下心来做自己能独立完成的事情,于是开始“翻译”(DeepL 机翻永远滴神) SuperMemo 网站上的 History of Spaced Repetition[8],了解起间隔重复的实践传统,而这离不开这一传统的塑造者,Wozniak 博士[9]。
SuperMemo 的创造者 Wozniak 是一个充满奇幻色彩的人。他富于激情,又固执傲人,History of Spaced Repetition 说是他的自传也不为过。巧合的是,他与我在学习上遇到的问题惊人的一致,对于一个追求极致效率的怪人来说,充满随机的遗忘和效率低下的复习是不可忍受的。Wozniak 以此为出发点,开始了他长达 30 年对记忆算法的追寻之路。而他的事业感染了我,让我觉得这是一项能从事终身的业行。
Woz 的记忆理论并不复杂,在他提出的记忆双组分模型[10]中,一条原子记忆在人脑中的状态可由两个变量来描述:
- 记忆可提取性
- 记忆稳定性
记忆可提取性其实就是在此刻我能够回忆起某条记忆的概率。为什么是概率呢?联想一下生活实际,遗忘并不是一个必然事件,今天我读到一本新书上的一个观点,我可能此刻还记得,但 10 天之后,我既不能保证我绝对记得,也不敢肯定我绝对会忘记。这是一个随机事件,那么就可以用概率来描述它了。
但记忆可提取性并不能完全描述记忆,就像光知道一辆汽车的开了多远,是无法知道这辆汽车何时能够到达目的地。光知道一条记忆此刻的回忆概率,也不知道什么时候会完全遗忘。因此,Woz 引入了记忆稳定性的概念,用于衡量遗忘的速度。而记忆可提取性、记忆稳定性和时间的关系,就可以通过以下公式刻画:
其中 R 是记忆可提取性,S 是记忆稳定性,t 是距离上次复习的时间,而这一公式正是遗忘曲线的数学模型。Woz 通过分析 SuperMemo 中收集到的数据,发现用指数函数来拟合记忆随着时间的衰减效果最佳。观察该公式,有一些简单的结论:
- 时间越长回忆起来的概率越低;
- 复习后遗忘的速度是先快后慢;
- 记忆稳定性越高遗忘得就越慢。
如此以来,记忆的遗忘情况就被刻画出来了。但它还无法对复习安排产生指导意义。为什么呢?因为这一模型遗漏了复习对记忆的影响。所以,在此基础上,Woz 又提出了记忆三变量模型:
通过观察数据,Woz 发现,复习时回忆成功就会提高记忆稳定性,而遗忘则会降低稳定性。但这样的定性分析对指导复习规划是远远不够的。我们还想知道提高了多少,或者降低了多少,为了便于讨论,不妨将其称为稳定性增长(上式中的 C)。Woz 认为,稳定性增长只与当前的记忆状态有关,即给定记忆稳定性和记忆可提取性,稳定性增长就确定了(其实就是马尔可夫链)。但理想很丰满,现实很骨感,数据并不完美支持 Woz 的理论,于是他打了个补丁,引入了第三个变量——记忆难度。在固定了记忆难度后,稳定性增长与记忆状态之间的关系就变得明晰了起来。
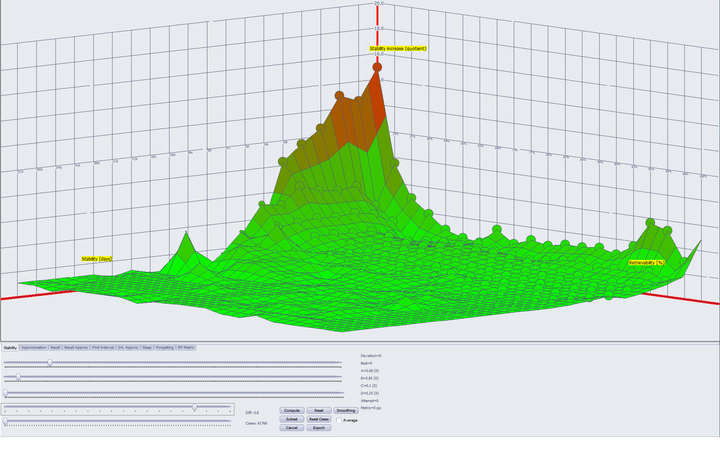
但在我看来,这只不过是转移了矛盾,因为在这之后还要找到记忆难度的变化规律。Woz 的后续研究也集中在难度的预测上,但恕我直言,玄学很多,数学很少。不过引入难度这一变量并没有错,本质上就是把原来的马尔可夫模型转化为了隐马尔可夫模型。(我第一次了解隐马尔可夫还是来自《如何用简单易懂的例子解释隐马尔可夫模型?》这篇知乎回答)
顺便补充一个我觉得很离谱的事儿,Woz 会在他的理论研究文章里讲他研究过程中的故事,比如人间蒸发一百天,在山中小屋中搞研究[11]。太有意思了。我也在阅读他的文章过程中受到他激情的感染。
进入业界
但空有激情不能成事,光研究传统理论也很难琢磨出什么创新与改进。自闭于传统之中,在理论上自娱自乐,并不能对世界做出什么实质的改变。最尴尬的是,记忆充满了不确定性,没有大量数据根本无法验证理论与自己的想法。但机缘巧合之中,在 2020 年的暑假,我投递了字节跳动的数据挖掘实习,简历被拒,隔天就在知乎上收到了墨墨背单词数据算法负责人的实习邀约。其中缘由,竟是他也在研究 SuperMemo 算法,然后在知乎上搜索到了我的翻译。被字节拒绝的我一看墨墨背单词有百亿复习数据,立马前往墨墨所在的城市——清远——一个像我老家宁德一样的地方,在业界中继续我的探索。


首先我将墨墨的数据在 SuperMemo 的理论上做了诸多验证,发现大部分规律都是一致的,这给予我一丝安慰和极大的信心。至少,我没有白研究那么久理论,同时,记忆的规律并不随着记忆者、记忆材料的更迭而改变的。然后,为了更好的研究记忆,我也推动着墨墨数据收集系统的改变。研究是一件难以预料和安排的事,如果研究的问题提得不对,那我可能从收集数据上就错了。Woz 总是惦记着他的记忆稳定性、记忆可提取性和记忆难度,我觉得他过早地简化了模型。若要对记忆进行更深入的分析,应当从最原始的数据开始。为此,我认为要记录完整的记忆数据,比如每一位用户每次复习的内容、时间、回忆成功还是失败、完整的复习历史等等。后来我才知道,其实我要记录的是记忆的时序信息,而这正是支持我研究记忆的基础。
独立思考
在深入研究记忆数据的过程中,我也逐渐发现了 Wozniak 的理论问题。在他的记忆三变量模型中,记忆稳定性和记忆可提取性都在墨墨的数据中找到了对应的模式。但记忆难度始终捉摸不透。另外他也缺少对高效复习的定义。这让我开始独立思考,尝试自己补上拼图中的空缺。
我的第一个切入点是通过模拟记忆过程来寻找最高效的复习策略。为此我根据 Woz 的理论和墨墨的记忆数据,在 2021 年年初编写了间隔重复模拟器[12],然后模拟各种策略的记忆情况,验证策略的效果[13]。首先我对复习过程做了诸多约束,比如固定每天的记忆总量,固定模拟时间跨度等等。然后以模拟结束后的记忆总量来衡量策略的效果。其实这就是蒙特卡罗模拟,虽然我并没有去系统的学习,但并不妨碍我去使用它。
在模拟验证过程中,我发现 Woz 的最大化记忆稳定性的策略并不是最高效的。这让我踏入了研究的空白区,我开始意识到记忆三变量模型也不足以支持我寻找高效记忆策略了,因为这个模型中并没有包含对记忆成本的约束。于是,在朦朦胧胧的直觉中,我自己定义了一个新的概念:复习压力。
我认为,高效的复习就是以最小的复习压力形成长期记忆。这里有一些直觉,比如随着每次复习成功,稳定性不断增长,复习压力会越来越小。那么复习压力肯定和复习次数有关。但两者之间的关系具体如何用数学语言描述,我那个时候的数学水平还不够,只好在草稿纸上不断地推演和尝试。在这个探索的过程中,我发现其实复习压力就是期望复习次数,而要计算着一期望,需要知道记忆的状态变化和复习策略。这一过程包括确定的模型和策略,也包括随机的遗忘。我想起我在知乎上读到过的一个数学工具正好能描述这一过程——随机过程。
找到了数学工具的我欣喜若狂,立马找到了 Ross 的 Introduction to Probability Models(实际上我是先找到了 stochastic process,但是太难懂了,看了这篇回答《请问下 Ross 的随机过程那个版本比较好?》后发现同个作者的另一本书更容易看懂),开始学习相关的知识。很快我就找到了一个和我脑海中复习压力计算非常相近的例题:

这道题是在说,一个矿工面对三个门,一个门走两个小时可以到达目的地,另外两个门分别走三小时和五小时回到原地,如果选门是等概率的,那么到达目的地所需时间的期望是多少。
可能你会奇怪,这个问题和复习压力有什么关系。我简单做一个类比,假设只有两个门,一个门叫做复习成功,一个门叫做复习失败,复习成功后记忆稳定性会增加,离形成长期记忆的目标就接近了一分,复习失败会导致记忆稳定性不增加(或下降),原地踏步或者离目标更远。每次选门都需要付出时间成本(复习需要时间),那么复习压力就是形成长期记忆所需要付出的总时间成本,也就是矿工达到目的地的期望时间。只不过记忆所面临的场景更加复杂,比如根据复习时间的不同,走进其中一个门的概率会发生变化,而且每次要走的门都可能是不一样的。但这两个问题的本质依然是一样的,很快我就操着这套数学工具把问题描述清楚了。

当一个模糊的现实问题被转化为清晰的数学问题,就已经成功了一半。但上述问题实际上是在给定复习策略的情况下计算复习压力期望,那么有没有什么问题是反过来,能求出期望复习压力最小的复习策略呢?我继续在随机过程中寻找工具,发现了马尔可夫决策问题。

本质上,复习安排优化就是在已知的记忆模型的基础上进行决策优化,最小化复习压力。但是 Ross 这本书并没有很详细地介绍如何优化决策。我只好在知乎上搜索马尔可夫决策过程相关的文章进行学习(比如这篇:《2.1.马尔可夫决策过程(MDP)》)。然后我搜索到了贝尔曼方程(这篇《马尔科夫决策过程之Bellman Equation(贝尔曼方程)》),发现这东西不就是动态规划吗?只不过加了点随机进去,要计算期望。
然后我又继续联想,发现如果我将记忆稳定性当作一系列离散的状态点,复习成本是他们之间的路径权重,回忆概率是这些路径走通的概率,那实际上这就是一个随机最短路问题。我很快就将我已有的动态规划知识和随机过程知识结合起来。然后我就写出了第一版迭代算法,可以用于计算每个记忆稳定性下最优的复习间隔对应的回忆概率。


至此,我认为我已经解决了优化复习策略的问题。开始着手对整个记忆规划系统进行梳理。
开始写作
第一篇论文
本质上,优化间隔重复调度可以分为两个部分,一是记忆建模,二是策略优化,我的第一篇论文《基于 LSTM 的语言学习长期记忆预测模型》就是聚焦于前者。
当时是 2021 年 9 月,我被抓回学校去做毕设,但我想在墨墨继续搞研究,于是和导师达成交易,我发表论文,他让我继续实习,于是我就花了大概一个月时间写第一篇论文。由于这是我第一次写学术论文,我就开始阅读相关文献。发现搞记忆建模的最近的一篇论文还是 Duolingo 在 2016 年发表的,我在知乎上总结了一篇笔记[14]。他们提出了一个记忆半衰期回归模型,其实就是用一些统计特征来预测记忆的半衰期。而记忆半衰期是什么东西呢?其实就是记忆稳定性。我轻车熟路地看完了他们的论文,发现可以改进的空间巨大。因为他们用的是统计特征,而记忆过程本质上是一个时序事件。那么用个时序特征+时序模型不就能水一篇论文了么。那最常用的时序模型,并且要和神经网络有关,那就非 LSTM 莫属了。
于是我就开始看 PyTorch 的文档,再抄抄别人在 GitHub 上写的 LSTM 调用代码,然后用 Pandas 和 Numpy 把墨墨的数据整理成可以输入 LSTM 的 Tensor,一周就把实验做完了。只是苦了我的 MacBook(还是用墨墨的实习工资买的),因为我一张显卡都没有。。。然后为了让我的论文和正统学术文献(Woz 的文章就像个民科写的)有个衔接,我把记忆稳定性都换成了记忆半衰期,记忆可提取性换成了回忆概率,模型也命名为了 LSTM-HLR,以表示我的工作是在 Duolingo 上的改进。
之后我又花了大概一周把论文初稿写完(中文版),论文的结构也是模仿 Duolingo 那篇论文。然后导师让我调研可以投稿的会议。搞笑的是,AI+教育交叉方向的会几乎都没有被 CCF 收录[15]。最后导师让我投了《中文信息学报》,十月份投稿,其中 rebuttal 一次,修改格式一次,十一月份就录用了。然后我就兴冲冲地回墨墨上班去了,当然名义也是非常正当了,这叫校外毕设,233。

第二篇论文
回墨墨后,我就把之前思考的复习策略给应用到真实业务上,进行了 AB 测试,效果喜人,多年来的研究终于有了回应,帮到了百万用户提高复习效率。我正打算继续优化算法,没想到导师又来找我了,大概是 2022 年 1 月左右。我以为他是询问我毕业论文写得咋样了,没想到他是搞偷袭,想要我再发一篇论文。说什么之前那个 CCF B 中文核心投中了很有优势,再发篇 CCF A 英文会议会更好之类的。其实我不是很想写了,但是考虑如果能发国际论文,可以让我的研究被更多人使用,也能帮助更多人,我就自我 push 了一下,开始了第二篇论文 A Stochastic Shortest Path Algorithm for Optimizing Spaced Repetition Scheduling 的写作。
这篇论文的主要是写复习策略优化的,为此我又看了不少文献,发现怎么大家这么喜欢强化学习,我对强化学习是不怎么感冒的,因为奖励很难设置,在墨墨背单词上搞在线强化学习也是很难落地的。直到我翻到了一篇用标记点过程和最优控制来做的文章,感觉里面的数学很优美(但我看不懂随机偏微分方程)。我就想着怎么用更优美的数学语言把我之前想到的最小复习压力迭代算法包装起来。正好那个时候我又在知乎搜索随机最短路相关的文章,找到了 《强化学习与最优控制》笔记(例如这篇:【强化学习与最优控制】笔记(二)随机性问题的动态规划)。简直如获至宝,原来最优控制理论已经有相关的数学工具来描述这个问题,我就把我之前的草稿写成 Bellman 方程的形式。

但是我又遇到了一个问题,那就是记忆模型该用什么。我的 LSTM-HLR 模型虽然已经被录用了,但是并没有被刊出,在新的论文里还得再介绍一遍,感觉会出问题。于是我把 Woz 的三变量模型搬了过来,并尝试用机器学习的方式去计算模型参数。在这个过程中,为了更好地观察记忆数据的规律,我先考虑如何将记忆时序数据进行降维。Woz 的 SInc 矩阵启发了我,可以将每个记忆行为用稳定性、可提取性、难度以及复习后的稳定性来表示。如果我们再把难度用颜色表示,那么剩下的三个属性就可以投影到 3-D 空间中。为此我又在网友的推荐下学了 plotly 这个数据可视化的库,然后对墨墨的数据一通操作:
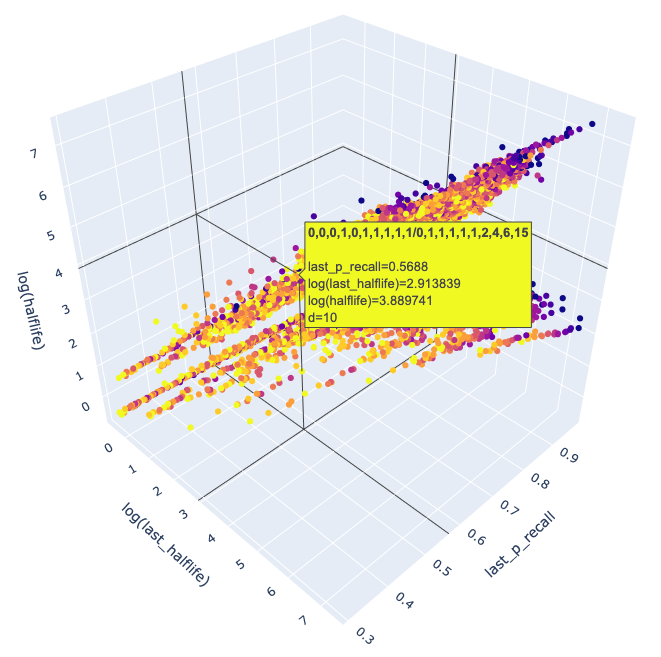
可视化之后,我发现一个简单的线性回归模型就足够了,最多再对特征做一些非线性变换。这里我参考了 Woz 的稳定性增长函数的形式。

然后这个人工时序模型就整出来了。接着就是拿去和 HLR 模型对比,发现效果确实好。这说明统计特征存在内在缺陷,其实这很好理解,忘记一次再记住一次,能和记住一次再忘记一次一样么?统计特征损失了时序信息,而时序信息在记忆状态的变化中又十分重要,所以效果好并不令我意外,意外的是之前居然没有人用时序信息来做记忆建模和预测。(其实是有的,但是年代太久远了,而且没有用到机器学习,他们参数怎么算的我都搞不懂)。后来发现原来记忆领域开源的数据集居然只有 Duolingo 一家的。为了能让论文更容易被别人复现,我和公司的负责人讨论了一下数据集开源的事儿,也算是为了这个领域能更进一步发展,最终决定公开数据集和实验代码:
Ye, Junyao, 2022, “Replication Data for: A Stochastic Shortest Path Algorithm for Optimizing Spaced Repetition Scheduling”, https://doi.org/10.7910/DVN/VAGUL0, Harvard Dataverse, V1
maimemo/SSP-MMC: A Stochastic Shortest Path Algorithm for Optimizing Spaced Repetition Scheduling (github.com)
回到这个时序模型,我继续看了一下《强化学习与最优控制》里面在已知状态转移方程的情况下,求解最优策略的方法,发现我之前写的迭代法就是 value iteration 方法,然后我就用伪代码包装了一下:

还挺像样的,J 就是成本矩阵, π 是策略矩阵,f 是记忆状态转移方程,d 是难度,h 是记忆半衰期,p 是回忆概率,a 和 b 是复习成功 or 失败的成本。通过不断遍历每个记忆状态下的复习间隔,计算期望复习成本,寻找最小化期望成本的复习间隔,不断迭代,最终就能收敛得到最优成本矩阵和最优策略矩阵。
这些内容写得差不多了之后,我就和导师同步了一下进度,我说我没用深度学习,是不是不好投,他说那你投 KDD 吧。然后我调研了一下 KDD,发现 KDD 还挺多企业在上面发论文的,而且有个专门的 applied data science track,我就开始按 KDD 的要求去改论文了。没想到 KDD 要双栏 9 页,我只好再加点酷炫的可视化图片进去,因为我听学长说没写满容易被认为不够 solid,笑死。
于是我就开始想有什么正当理由来加可视化图片,我就联想到之前一堆深度强化学习方法都是黑箱,可解释性不高,我可以以解释模型机制为由,去可视化一下模型的权重和最优策略的模式:
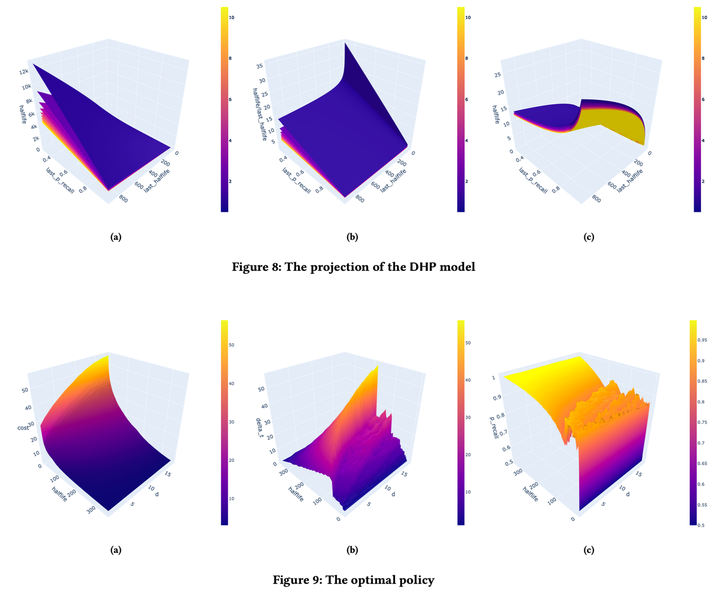
然后看图说话就完事了,这里说几个从记忆模型观察到的结论:
- 随着难度增长,半衰期的增长潜力在不断下降
- 随着回忆概率下降,半衰期的增长潜力会上升,这意味着「值得的困难」
- 随着半衰期增长,半衰期的增长潜力会下降,也就是说记忆无法无限地巩固下去
还有从最优复习策略中观察到的现象:
- 难度越高,期望复习成本也越高
- 期望复习成本随着半衰期增长而下降
- 半衰期相同时,最优的复习间隔随着难度增长
后面为了把时序模型和随机最短路问题用直观的方式展示出来,又拿 http://draw.io 画了一下流程图:
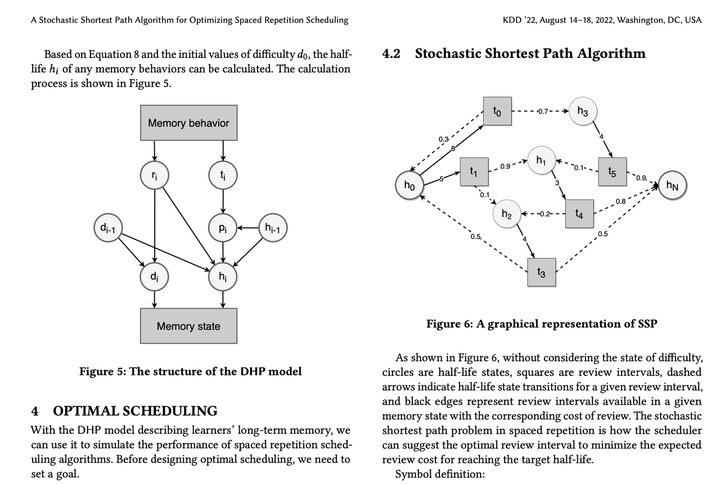
顺带一提,这是我第一次用英文写学术论文,非常痛苦,为此看了不少知乎上的论文写作教程(比如 《怎样写好英文论文的 Introduction 部分?》、《DrustZ的论文小课堂 [相关工作Related Work]》和《有没有比 Grammarly 更先进的英语作文修改润色软件?》)DeepL + Grammarly + QuillBot 救我于水火之中!
然后就是和导师一起改论文,最终在 2 月份过年的时候赶上了 ddl,交了稿。然后 5 月份收到了录用通知,这里的故事差不多就结束了。
彩蛋
但是故事还没完,四月底的时候导师又来找我了,说 KDD 挺难中的,让我再准备一篇 NIPS。。。结果才准备半个月,刚写完初稿,KDD 中了,我导师改口说咋们拓展成英文期刊论文吧。所以我这两个月又在写期刊论文,双栏 12 页写得我头皮发麻。不过还是写完了,并且把我之前的构思也加进来了,希望今年能投中吧。
总结
回顾我的研究历程,充满了各种巧合和意外,我不敢说我在这一研究中作出了多么突出的贡献。没有 Anki 的帮助,Wozniak 的理论,墨墨背单词的数据,知乎用户产出的各类学习资料,这项研究都无法继续。
但有一点不可否认:我选择了自己的道路,在探索中自由学习,在激情的驱动下不断前行,并想方设法地摆脱学校的控制。
我坚信对记忆的研究能推动教育技术的发展,让更低成本的学习工具到达每一位学习者手中。
我通过自由学习找到了自己的人生道路,从一名小镇做题家转变为教育科技企业的算法工程师,成为记忆领域的科研工作者。我相信在未来,每一个学生都能挣脱腐朽的强制学校教育的束缚[16],通过自由学习实现自我[17],也过上世俗意义上的好日子。
最后,也希望各位读者能够找到自己愿意付出一生的研究事业。愿意来和我一起做间隔重复记忆研究那就更好了哈哈。
以下是一些研究资源汇总:
Thoughts Memo:[开源+墨墨背单词] 时序记忆行为数据集介绍叶峻峣:目前世界最大的人类记忆行为数据集发布Thoughts Memo:间隔重复记忆算法研究资源汇总
https://www.zhihu.com/question/870573710/answer/7848446713
转载请注明:乐无限,互联网有趣资源聚合地 » 如何找到愿意为之付出一生的研究事业?